科研进展 | 基于对数老化随机过程理解远离平衡态系统的超慢动力学和普适老化现象

虽然线性响应理论在描述近平衡态系统的动力学特征方面取得了显著成功[1]，亚扩散随机过程也被广泛应用于刻画动力学临界现象[2]，然而，这些理论在理解远离平衡态系统中普遍存在的超慢弛豫动力学和老化现象[3-6]方面面临挑战，而这正是理解非平衡态系统动力学的关键难题。

近期，李春艳、刘海文教授与谢心澄院士合作，提出了基于对数老化随机过程（如图1所示，该过程的演化显著依赖于系统过去的完整历史）的普适性理论框架[7]，旨在描述远离平衡态系统中的超慢动力学和老化现象。研究发现，这种新型随机过程能够有效地刻画Anderson玻璃态的对数老化特征，并成功描述了Griffiths-McCoy奇异性的动力学特征。这类新奇的Griffiths-McCoy奇异性既可在经典系统中出现，也可在量子系统中存在，在量子系统中常被称为量子Griffiths奇异性。值得一提的是，谢心澄院士和刘海文教授的前期研究，并与实验合作者合作发现，量子Griffiths奇异性广泛存在并主导了二维超导金属相变的量子临界行为[8-14]。因此，针对对数老化随机过程的分析和模拟，为理解和刻画远离平衡态体系的复杂动力学特征提供了一条全新的研究路径。

该项研究揭示了对数老化随机过程的两个关键动力学特征：（1）系统的生存概率和返回概率均呈现出对数依赖于时间的行为，即（如图2所示，其中为系统老化时间）。生存概率的这种特征成功解释了在Anderson玻璃态中观测到的电导率的对数老化现象[3]。（2）研究发现，对数老化随机过程的位置自关联函数具有幂律形式的衰减（如图3所示），其中指数 β 可以非常小。这种动力学行为与Griffiths-McCoy奇异性中关联函数的行为高度相似[15]。该研究团队的后续系列研究进一步揭示了对数老化随机过程与Griffiths-McCoy奇异性之间存在的深刻内在联系。

该项研究成果近期以“Route of Random Process to Ultraslow Aging Phenomena”为题发表在国际著名期刊《物理评论快报》（Physical Review Letters）上[7]。北京师范大学博士生李春艳为第一作者，刘海文教授为通讯作者，谢心澄院士提供了重要的理论指导。该研究工作得到了国家重点研发计划、国家自然科学基金委、中国科学院战略性先导科技专项以及中央高校基本科研业务费的资助。

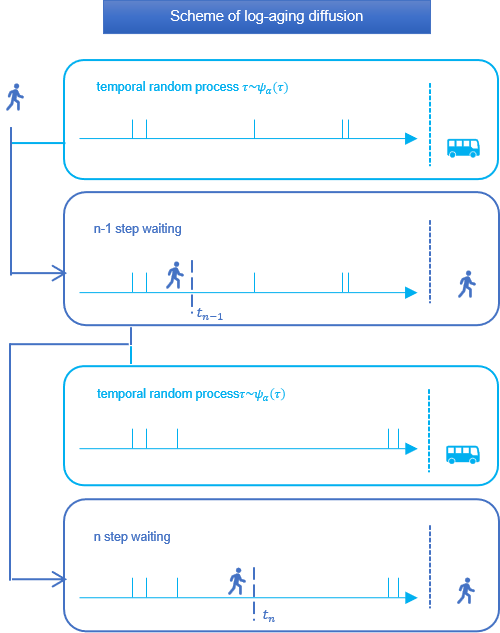
图1 | 我们通过一个乘客等公交的场景来展示对数老化扩散过程。每个公交站的发车间隔时间遵循长尾分布。当乘客到达第
站时，他们经历了的等待时间。一旦公交车抵达第站，乘客迅速上车并前往下一站，其行程时间远小于等待时间。到达第站后，乘客开始等待下一班车，并记录等待时间为。

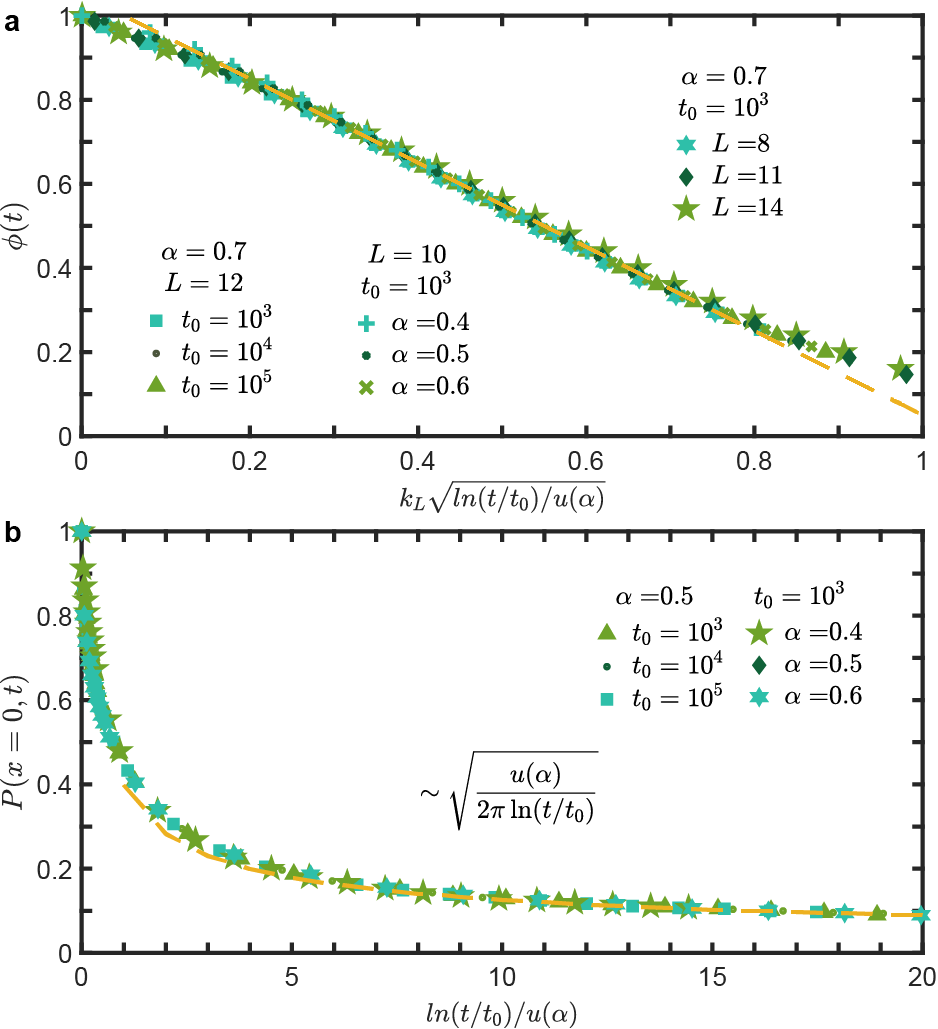
图2 | (a) 在一维晶格（长度 L，晶格间距 a=1）上，单个粒子在初始时间开始进行对数老化扩散的模拟存活概率 ϕ。(b) 模拟初始时刻位于原点的粒子返回原点的概率 P(x=0,t)，以揭示其随时间返回初始位置的可能性。

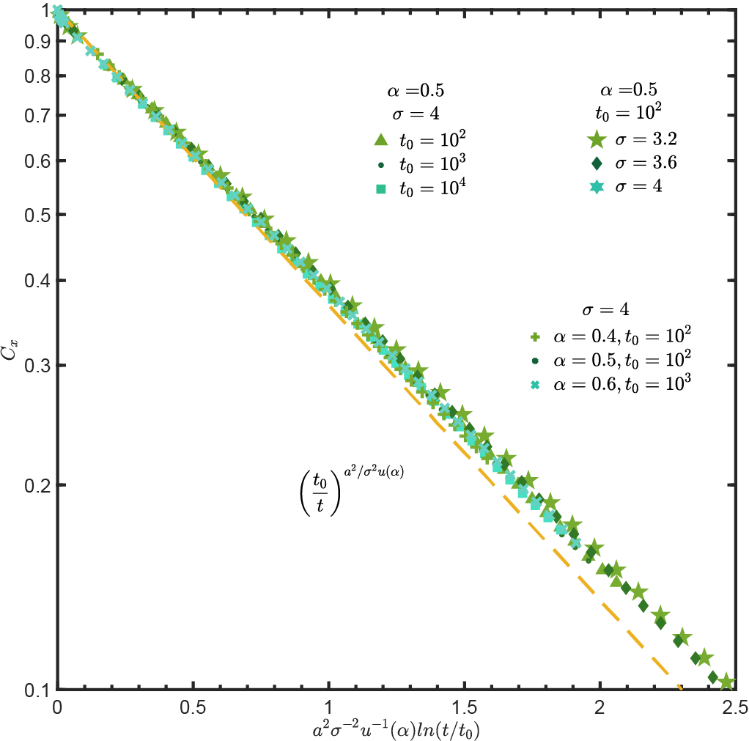
图3 | 研究在谐振势中(])，粒子在一维晶格（晶格间距 a=1）中对数老化随机扩散的自相关函数特征。

[1] R. Kubo, Statistical-mechanical theory of irreversible processes I,  Journal of the physical society of Japan, 12, 570 (1957).

[2] U. C. Täuber, Critical dynamics, Cambridge University Press (2014).

[3] V. Orlyanchik and Z. Ovadyahu, Stress aging in the electron glass, Phys. Rev. Lett. 92, 066801(2004).

[4] D. Shohat, Y. Friedman, and Y. Lahini, Logarithmic aging via instability cascades in disordered systems, Nat. Phys. 19, 1890 (2023).

[5] Y. Kaplan, et al., Observation of universal ageing dynamics in antibiotic persistence, Nature 600, 290 (2021).

[6] M. A. Lomholt, L. Lizana, R. Metzler, and T. Ambjörnsson, Microscopic origin of the logarithmic time evolution of aging processes in complex systems, Phys. Rev. Lett. 110, 208301 (2013)

[7] C. Li, H. Liu, and X. C. Xie, Phys. Rev. Lett. 134, 197102 (2025).

[8] Y. Xing, et al., Quantum Griffiths singularity of superconductor-metal transition in Ga thin films, Science 350，542 (2015).

[9] H. Ji, H. Liu, H. Jiang and X. C. Xie, Disorder effects on quantum transport and quantum phase transition in low-dimensional superconducting and topological systems, Advances in Physics: X 6, 1884133 (2021).

[10] Y. Liu, et al., Anomalous quantum Griffiths singularity in ultrathin crystalline lead films, Nature Commu. 10, 3633 (2019).

[11] Y. Liu, et al., Observation of In-Plane Quantum Griffiths Singularity in Two-Dimensional Crystalline Superconductors, Phys. Rev. Lett. 127, 137001 (2021).

[12] Q. Zhao, et al., Isotropic Quantum Griffiths Singularity in Nd0.8Sr0.2NiO2 Infinite-Layer Superconducting Thin Films, Phys. Rev. Lett. 133, 036003 (2024).

[13] S. Qi, et al., Quantum Griffiths Singularity in a Three-Dimensional Superconductor to Anderson Critical Insulator Transition, Phys. Rev. Lett. 133, 226001 (2024).

[14] Effectively tuning the quantum Griffiths phase by controllable quantum fluctuations, Science Advances 10, eadp1402 (2024).

[15] F. Iglói and H. Rieger, Random transverse Ising spin chain and random walks, Phys. Rev. B 57, 11404 (1998).

论文链接：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.197102